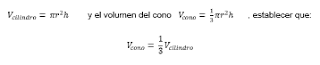3D World: 2015

“EVOLUCION HISTORICA DEL CALCULO DEL VOLUMEN DE LOS CUERPOS GEOMETRICOS”

AREA Y VOLUMEN A TRAVES DE LA HISTORIA

La historia del inicio de la geometría, es muy similar a la historia del origen de la aritmética, siendo esta una consecuencia de aplicaciones en actividades prácticas, es decir, la geometría nace en el intento de dar soluciones a problemas de la vida cotidiana. El primer acercamiento del hombre a la geometría fue a partir de observaciones realizadas a su entorno natural, descubriendo de este modo las primeras formas geométricas.

Herodoto (historiador y geógrafo griego considerado como el padre de la historiografía) atribuyó el descubrimiento de la geometría a los egipcios, ya que, según él, ellos necesitaban medir constantemente la superficie de sus tierras debido a que los desbordamientos anuales del río Nilo borraban continuamente las señales que limitaban los terrenos de los agricultores, es decir el rio al desbordarse borraba las fronteras de sus tierras. De hecho, la palabra geometría proviene del griego geo (tierra) y métrica (medida), es decir medición de la tierra.

En Egipto el cálculo desarrollado en el área de la geometría se centró principalmente en el cálculo de áreas y volúmenes, sin embargo el desarrollo geométrico carece de demostraciones formales.

Después de ver las grandes construcciones que se llevaron a cabo en el antiguo Egipto podríamos esperar un estudio muy avanzado de la geometría, no obstante las únicas fuentes que podemos analizar son el papiro Ahmes y el papiro de Moscú. Con los datos obtenidos de estos dos papiros no se han podido descubrir aspectos especiales de la geometría, siendo los aspectos que más resaltan, algunos datos que les permitieron calcular áreas y volúmenes de figuras y cuerpos considerados muy básicos. Los cálculos, aunque incorrectos si son lo suficientemente aproximados para cubrir las necesidades de la vida cotidiana. Por otro lado, no existe distinción entre los cálculos exactos y los cálculos aproximados, por lo que es difícil entender si ellos consideraban todos sus cálculos como exactos o sencillamente no se planteaban la posibilidad de que existiera algún error cometido, algunos de estos errores son realmente importantes, pero quizá fuese el hecho de haber aprendido a realizar los cálculos sin demostraciones de ningún tipo y sin cuestionar sus procedimientos y resultados lo que les llevaba a cometer estos errores.

En primer lugar hay que tener en cuenta que hasta la llegada de los griegos, al igual que en Babilonia, no existía una separación de contenidos entre la geometría y la aritmética, o en la matemática en general, y todas las ramas se englobaban dentro de una misma limitándose a aplicar la aritmética al cálculo de áreas, volúmenes y cualquier otro tipo de problema geométrico que se les presentase.

En los muros del templo de Edfu aparece este método, que consistía en obtener el área de una figura de cuatro lados multiplicando entre si las semisumas de las longitudes de lados opuestos. Se dice que para calcular el área de un campo de lados a, b, c, d, siendo a, b y c, d los lados opuestos, se siga la siguiente regla:

Evidentemente esta fórmula es exacta para figuras rectangulares, pero cuanto más irregular sea la figura, más inexacto será el resultado. Este método también fue empleado para calcular campos triangulares, en los que se afirma que debe considerarse el lado d como “nada”.

En el papiro Ahmes podemos observar que para realizar el cálculo de áreas, los egipcios tendían a intentar convertir la figura analizada en “algo similar a una de las figuras conocidas” ya que este método permitía obtener el área buscada. De hecho este fue el método que emplearon para calcular el área del círculo, el cual quizá fue uno de los primeros pasos hacia las demostraciones geométricas y un intento para encontrar las relaciones existentes entre las figuras geométricas, lamentablemente se quedó ahí, en los primeros pasos.

Según Ahmes, se puede calcular el área de un triángulo dividiendo su base por la mitad y multiplicando el resultado obtenido por la altura de dicho triángulo. Aunque si bien en el papiro el escriba no empleó los términos base o altura para expresarse, pero por la figura y la explicación que da entendemos la figura como un triángulo isósceles. Ahmes justifica los cálculos realizados afirmando que el triángulo se puede descomponer en dos triángulos rectángulos, de modo que el desplazamiento de uno de ellos da lugar a un rectángulo con lados de la misma longitud que el triángulo que se tenía inicialmente.

En el papiro Ahmes se describe el triángulo como: “un pedazo de tierra de una cierta anchura en un extremo y que llega a un punto”. En Ahmes cuando se habla de altura en verdad se emplea un término genérico conocido como “línea”, afirmando que debe multiplicarse la base por la línea. No queda claro si en verdad el escriba se refería a la altura o a uno de sus lados.

En el mismo papiro podemos ver que en el problema 52 se trata el cálculo del área de un trapecio isósceles cuya base mayor mide 6 unidades, la base menor mide 4 unidades y la “distancia” es de 20 unidades. Para resolverlo calculan la semisuma de las bases con la intención de transformarlo en un rectángulo y esta semisuma la multiplican por la “distancia”.

Quizás sea el cálculo del área del círculo la parte de la geometría egipcia de la que más se ha escrito, dado que ha sido para muchos el mayor éxito de los escribas egipcios y también por todo el misterio que implica al número pi. El sistema que ellos empleaban consistía en sustraer un noveno del diámetro de la circunferencia y calcular la superficie del cuadrado correspondiente, lo que nos da u valor para pi de 3,1605, esta información podemos encontrarla en el papiro Rhind en el problema 50 en el cual Ahmes acepta que el área de un circulo de diámetro nueve es la misma que la de un cuadrado de lado ocho. El valor obtenido por ellos para pi resulta ser una muy buena aproximación para el valor real el cual es aproximadamente 3,1416. Teniendo en cuenta el hecho de que los escribas egipcios no consideraban el valor de pi como una constante no se sabe en la actualidad que fue lo que los llevo a obtener la aproximación ya mencionada, aunque se ha considerado que en el problema 48 se encuentra la respuesta a esta incógnita. En este problema Ahmes construye un octógono a partir de un cuadrado de lado nueve unidades. Mediante una serie de cálculos llegaron a la conclusión de que el área de un octógono es aproximada al área del círculo de diámetro nueve.

Otro hecho notable del trabajo realizado por los egipcios además de la buena aproximación obtenida para el valor de pi es la siguiente afirmación: “la razón entre el área de un circulo y su circunferencia es la misma que la razón entre el área y el perímetro del cuadrado circunscrito a ella.”

Existen numerosas leyendas en torno a las relaciones geométricas existentes en la construcción de las pirámides. Probablemente la más llamativa y conocida es aquella en la que se afirma que el perímetro de la base de la pirámide coincide con el diámetro de una circunferencia cuyo radio es la altura de dicha pirámide. Esta relación es efectivamente cierta con una muy buena aproximación para el valor de pi, ya que la razón del perímetro y la altura es de:

que nos da un valor para pi de 3.1429 y no el valor de 3.1605 que aparece en los papiros y que sabemos por los mismos que era el valor que empleaban. Estas afirmaciones en torno al valor de pi solo son especulaciones, dado que los escribas egipcios no empleaban a pi como un valor constante y posiblemente el propio concepto y su relación con el círculo les era algo desconocido, ya que no lo aplicaban por ejemplo al calcular el volumen de un cilindro.

Del mismo modo que la división de las superficies para repartir los terrenos generó la necesidad de conocer el cálculo de diversas superficies, el almacenamiento del grano, dio lugar al cálculo de volúmenes de graneros tanto rectangulares como circulares. El cálculo de estos volúmenes dependía igual que en la actualidad de la base elegida para edificar los graneros.

El caso del cálculo del volumen de los graneros de base rectangular aparece en el problema 44 del papiro de Rhind, existen otros problemas similares los cuales son el problema 45 del mismo papiro y los problemas 30 y 32 del papiro de Kahún. Las resoluciones planteadas en todos los problemas encontrados llevan a deducir que conocían la fórmula del volumen para un granero de base rectangular tal y como la conocemos ahora:

Donde a y b son los lados de la base de la pirámide de base rectangular y h la altura de esta.

En particular el cálculo del volumen de una pirámide lo obtenían de la formula anterior considerando a = 0

Así como aparecen en los papiros métodos para calcular el volumen del tronco de una pirámide, existe también un método para calcular el volumen de un cono truncado, esta es la siguiente:

Donde h corresponde a la altura del cono truncado, D el diámetro del círculo más grande y d el diámetro del círculo más pequeño.

Lógicamente no existe en los papiros una formulación tal como se ha expuesto anteriormente, sino que se explican los casos con ejemplos donde se dice “divide 18 entre 12, suma 7 y 4, etc.” El método visto para calcular el volumen de un cono truncado supone considerar un valor para pi de 3, en comparación al valor encontrado de 3,1605 empleado en el cálculo de áreas, lo cual supone un error considerable que nos lleva a pensar en el empleo de métodos empíricos para llegar a tales conclusiones, puesto que lo que si podemos afirmar es que no se empleaba pi como constante, por lo que hemos de deducir que tampoco conocían su relación con el perímetro o el área del círculo.

No se conoce el cómo los antiguos egipcios pudieron llegar a estos resultados, se ha afirmado que podría tener su origen en métodos experimentales, pero desde luego no es un método que resulte fácil. Para el cálculo del volumen del tronco de pirámide parece más viable que descompusieran el tronco en cuerpos más sencillos como lo son prismas, pero ciertamente no existen indicios que lo demuestren ya que no hay vestigios de aquello, por lo que aparentemente el uso de la geometría basada en descomposiciones no parece haber prosperado en el antiguo Egipto y esto deducido de los métodos que empleaban para el cálculo de áreas de triángulos y trapecios.

A pesar de que según Herodoto, la geometría se desarrolló ante la necesidad de recalcular las lindes tras las inundaciones del rio Nilo, no parece que sea enteramente así. Indudablemente esta era una de las aplicaciones más importantes pero desde luego no era la única. Los babilonios por ejemplo tenían una geometría muy similar a la desarrollada en Egipto y sin embargo no tenían la necesidad de agrimensura.

Los babilonios utilizaban para calcular áreas y volúmenes muchas fórmulas más o menos exactas. Para calcular el área de un cuadrilátero realizaban la multiplicación entre las medias aritméticas de los pares de lados opuestos al igual que los egipcios. Para realizar el cálculo del volumen del cono truncado desarrollaron la siguiente formula:

Donde a y b corresponden a las áreas de los círculos de las bases. Para el tronco de una pirámide emplearon la siguiente formula:

Donde a y b corresponden a los lados del rectángulo de la base de la pirámide y h corresponde a la altura de esta.

El cálculo realizado para obtener el volumen de un cilindro era tal y como lo conocemos el día de hoy, con una diferencia, multiplicando el área de la base por la altura, la diferencia la encontramos en el método que empleaban para realizar el cálculo del área del círculo.

El cálculo realizado para obtener el área de la base es correcto considerando un valor aproximado de pi a 3. En esta fórmula h corresponde a la altura del cilindro y el área de la base, y d el diámetro del circulo de la base del cilindro.

Si nos trasladamos a la cultura India podemos notar que dada su costumbre de transmitir sus conocimientos verbalmente se ha dificultado enormemente la investigación del origen de la geometría en su territorio. Los pocos indicios encontrados nos señalan que los hindúes conocían la construcción de figuras como cuadrados, círculos y triángulos entre otros, sabían calcular áreas empleando conceptos de semejanza y proporción con procedimientos muy similares al empleado por Thales de Mileto. Podían calcular el volumen de cuerpos sencillos como prismas y tenían un método para el cálculo del volumen del tronco de pirámide, con elementos propios de la cultura babilónica lo cual indica una fuerte influencia de esa cultura.

En China, el emperador Qin Shi Huang (Shi Huang-ti) ordenó en el 212 a. C. que todos los libros de fuera del estado de Qin fueran quemados. El mandato no fue obedecido por todo el mundo, pero como consecuencia se conoce muy poco acerca de la matemática en la China ancestral.

Desde la Dinastía Zhou, a partir del 1046 a. C., el libro de matemáticas más antiguo que sobrevivió a la quema fue el I Ching, que usa trigramas y hexagramas para propósitos filosóficos, matemáticos y místicos. Estos objetos matemáticos están compuestos de líneas enteras o divididas llamadas yin (femenino) y yang (masculino), respectivamente (véase Secuencia del Rey Wen).

La obra más antigua sobre geometría en China viene de canon filosófico mohista, hacia el 330 a. C., recopilado por los acólitos de Mozi(470-390 a.c.). El Mo Jing describió varios aspectos de muchos campos relacionados con la física así como proporcionó una pequeña dosis de matemáticas.

Después de la quema de libros, la dinastía Han (202 a.C - 220 d.C) produjo obras matemáticas que presumiblemente abundaban en trabajos que se habían perdido. La más importante de estas es Los nueve capítulos sobre el arte matemático, cuyo título completo apareció hacia el 179 d. C., pero existía anteriormente en parte bajo otros títulos. La obra consiste en 246 problemas en palabras que involucran agricultura, negocios, usos geométricos para establecer las dimensiones de las pagodas, ingeniería, agrimensura y nociones sobre triángulos rectángulos y π. También se usa el Principio de Cavalieri sobre volúmenes más de mil años antes de que el propio Cavalieri lo formulara en Occidente. Se crearon pruebas sobre el Teorema de Pitágoras y una formulación matemática de la eliminación de Gauss-Jordan. Liu Hui hizo un comentario de la obra hacia el siglo III d. C.

En el siglo tercero después de nuestra era vivió Liu Hui quien comento los nueve capítulos y calculó para pi un valor de 3,14 utilizando un polígono regular de 96 lados, posteriormente calculó pi con un valor de cinco cifras decimales correctas 3,14159 utilizando un polígono de 3072 lados.

Las obras matemáticas del Han astrónomo e inventor Zhang Heng (78–139 D.C.) contenían una formulación para pi también, la cual difería de los cálculos de Liu Hui. Zhang Heng usó su fórmula de pi para encontrar volúmenes esféricos.

Zu Chongzhi (siglo V) de las Dinastías del Sur y del Norte calculó el valor de π hasta siete lugares decimales, lo que daba lugar al valor de π más exacto durante casi 1000 años.

Como hemos podido apreciar, en la antigüedad distintas culturas intentaron dar respuesta al problema del cálculo del volumen de distintos cuerpos geométricos, sin embargo no es hasta los siglos VI y IV antes de cristo que floreció en Grecia la escuela científica y filosófica más importante de su época ya que es aquí donde se comienza a formalizar el conocimiento geométrico, ya que los griegos no se limitaron a observar algunas relaciones interesantes entre los números y las figuras geométricas o a usarlas en sus mediciones y construcciones para resolver problemas de cálculo, sino que fueron los primeros en darse cuenta de la importancia de encontrar enunciados generales y demostrarlos. Elaboraron así con el paso del tiempo, una geometría independiente de los casos concretos, construyeron el primer sistema de matemáticas puras, matemáticas que se han empleado hasta nuestros días.

La geometría fue la primera rama de las matemáticas y se consolido gracias, fundamentalmente al trabajo de Euclides, quien en su obra titulada “Los Elementos” reunió todo el conocimiento matemático de su época, lo organizo, y lo más importante, lo formalizó.

Se realizaron importantes aportes para el cálculo del volumen de cuerpos como prismas y pirámides, cuyas formulas son las siguientes:

Donde A sub b es el área de la base y h es la altura del cuerpo correspondiente, si bien es cierto que otras civilizaciones habían obtenido formulas acertadas para estos tipos de cuerpos en algunos casos, fueron los griegos los primeros en formalizarlos.

En la antigua Grecia (287-212 antes de Cristo) aparece un personaje muy importante en la historia del cálculo del volumen de los cuerpos geométricos, Arquímedes de Siracusa, quien es famoso por el origen de la palabra ¡Eureka!, cuenta la historia que Arquímedes pronunció esta palabra tras descubrir que el volumen de agua ascendido era igual al volumen del cuerpo sumergido. Esto le llevó la solución al problema de medir el volumen de cuerpos irregulares y le permitió saber si la corona del rey Hierón II estaba hecha de oro puro al calcular su densidad a partir de la masa ya conocida. Este descubrimiento lo habría realizado mientras se encontraba sumergido en la bañera y tal fue su alegría que salió corriendo a las calles de Siracusa desnudo y gritando ¡Eureka! (‘¡Lo he descubierto!’). Si bien este descubrimiento fue muy importante no es el único descubrimiento que podemos atribuirle en torno al tema que nos convoca, ya que él es también responsable de una aproximación de pi por exceso y por defecto y por ende dado que el cálculo del volumen de cuerpos redondos como son el cilindro y el cono están directamente relacionadas con el numero pi, entonces podemos relacionarlos a Arquímedes, las fórmulas para calcular dichos volúmenes son:

Donde r es el radio y h corresponde a la altura. Luego fue Arquímedes quien a partir del volumen del cono y diversos cálculos pudo obtener el volumen de la esfera:

Lo cual corresponde a cuatro veces el volumen de un cono que tiene por base el círculo máximo de la circunferencia y de altura el radio de la misma.

Además introduciendo una esfera en un cilindro de igual radio descubrió las relaciones entre las áreas y los volúmenes de ambos cuerpos, empleando sus propias palabras: “cualquier cilindro que tenga como base el circulo máximo de una esfera y la misma altura que la esfera tiene por volumen una vez y media el de la esfera”

Para obtener esta relación Arquímedes partió de una semiesfera de radio R y colocó a su lado un cono recto y un cilindro circular recto, ambos con base de radio también R:

Esta imagen muestra como realizo Arquímedes el trabajo que lo llevó a obtener la relacion entre el volumen de la esfera, el cono y el cilindro

Cortó las tres figuras con un plano paralelo a la base del cilindro (que quedara a distancia de la parte superior de las tres figuras) y estudió cómo serían las secciones que este plano crearía en cada una de las figuras:

Cilindro: circunferencia de radio R.
Semiesfera: también una circunferencia pero de distinto radio, digamos r. Mirando la siguiente figura

y usando el teorema de Pitágoras tenemos que r²+d²=R².

Cono: también una circunferencia, pero ahora, como podemos se ve aquí

El radio es d.

Por tanto tenemos:

Sección cilindro=πR²=π(r²+d²)=πr²+πd²=Sección semiesfera+Sección cono

Las secciones de cada figura son como rebanadas de las figuras:

Si para cada rebanada se tiene la relación anterior parece bastante claro que los volúmenes siguen la misma relación. Es decir:

Volumen cilindro = Volumen semiesfera + Volumen cono

Pero Arquímedes conocía los volúmenes del cilindro y del cono:

De donde multiplicando por 2 obtenemos el volumen de una esfera de radio R:

Tanto admiraba Arquímedes este descubrimiento que mandó inscribir en su tumba la siguiente imagen:

Después de Arquímedes pasaron muchos años hasta que aparecieron nuevos planteamientos respecto al cálculo del volumen de los cuerpos geométricos. Si bien es cierto durante el siglo anterior a Newton y Leibniz, los trabajos de los matemáticos griegos se hicieron populares, especialmente los trabajos de Arquímedes. Se desarrollaron técnicas infinitesimales para calcular áreas y volúmenes. Kepler fue uno de los matemáticos que contribuyeron a estos desarrollos. De un modo anecdótico podemos decir que su interés por el cálculo de áreas y volúmenes surge a partir de un incidente que ocurrió cuando se casó por segunda vez. Kepler había comprado un barril de vino para su boda y el procedimiento que empleó el mercader de vino para medir el volumen del barril enfadó a Kepler. A partir de este incidente, estudió cómo calcular áreas y volúmenes de diferentes cuerpos, especialmente cuerpos de revolución, y escribió un libro sobre el tema. Ésta fue su principal contribución al origen del cálculo integral.

Kepler estudió los trabajos de Arquímedes y escribió un libro (publicado en 1615): "Nova Estereometría doliorum vinariorum" (Nueva Geometría sólida de los barriles de vino).

Es un trabajo sistemático en el que se usan técnicas infinitesimales para el cálculo de áreas y volúmenes. Se concentra en los sólidos de revolución e incluye el cálculo (exacto o aproximado) de más de noventa sólidos. Actualmente usamos cálculo integral para resolver este tipo de problemas.

En su trabajo, Kepler desarrolla los procedimientos de Arquímedes (aunque en su tiempo no se conocía "El Método" de Arquímedes, pues estaba perdido) El enfoque de Kepler en su estereometría es diseccionar un sólido en un número infinito de piezas infinitesimales, o sólidos "indivisibles", de una forma y tamaño conveniente a la solución de cada problema particular. Entonces suma todos esos indivisibles de alguna manera para obtener el área o volumen de la figura dada.

Los elementos infinitesimales de Kepler tienen la misma dimensión que el cuerpo que quiere medir. Si quiere calcular un área, suma elementos área y si quiere calcular un volumen considera elementos infinitesimales con volumen.

"Pensó en el volumen de un barril, como el de cualquier otro cuerpo, como formado por numerosas hojas finas adecuadamente dispuestas en capas, y considera el volumen del barril como la suma de los volúmenes de estas capas, siendo cada una de ellas un cilindro."

Veinte años después de la publicación de la Estereometría doliorum de Kepler se publicó un libro en Italia que rivalizó con él en popularidad: Geometría indivisibilibus de Bonaventura Cavalieri (1635)

En este libro, el matemáticos italiano usó lo que ahora conocemos como Principio de Cavalieri: Si dos sólidos tienen las alturas iguales y si las secciones hechas por planos paralelos a las bases a la misma distancia de la base están en una determinada proporción, entonces los volúmenes de los sólidos están también en esa proporción.

El Principio de Cavalieri se conoce también como el método de los indivisibles. "Cavalieri hizo de la noción de indivisible la base de un método geométrico de demostración. No explicó precisamente lo que entendía por la palabra indivisible que empleó para caracterizar los elementos infinitesimales que usó en su método. Cavalieri concibió una superficie como formada por un número indefinido de líneas paralelas equidistantes y un sólido como compuesto por planos paralelos equidistantes, y designa estos elementos los indivisibles de la superficie y del volumen respectivamente." (C.H. Edwards)

Zu Geng, que nació hacia el año 450, fue un matemático chino que usó lo que conocemos como el Principio de Liu Hui y Zu Geng para calcular el volumen de una esfera. La teoría de Liu-Zu es equivalente al Principio de Cavalieri. Es decir, matemáticos chinos han usado este principio más de mil años antes que Cavalieri.

Una aplicación bien conocida del Principio de Cavalieri nos permite calcular el volumen de una esfera. Podemos comparar el área de una sección de un hemisferio y el área de una sección de un cuerpo que es un cilindro menos un cono. Estas dos áreas son iguales. Entonces los dos cuerpos tienen el mismo volumen. Es fácil calcular el volumen de este segundo cuerpo, y así obtenemos el volumen del hemisferio.

El método de Cavalieri es diferente al de Kepler en dos aspectos importantes:

"En primer lugar, Cavalieri procede estableciendo una correspondencia uno a uno entre los elementos indivisibles de dos figuras geométricas dadas. Si los indivisibles correspondientes de estas dos figuras están en una cierta proporción (constante), entonces concluye que las áreas o volúmenes de las figuras están en la misma proporción. Típicamente, el área o volumen de una de las figuras se conoce por adelantado y así obtenemos el de la otra.

En segundo lugar, Kepler considera una figura geométrica compuesta por indivisibles de la misma dimensión. Sin embargo, Cavalieri generalmente considera una figura geométrica compuesta por un número infinitamente grande de indivisibles de dimensión menor. Un área está formada por segmentos paralelos y equidistantes y un volumen consiste en secciones planas paralelas y equidistantes.

Cavalieri hace de la noción de indivisible la base de su método geométrico de demostración. No explicó que entendía precisamente con la palabra indivisible que él empleó para caracterizar los elementos infinitesimales que usa en su método. Cavalieri concebía una superficie como formada por un número indefinido de líneas paralelas equidistantes y un sólido como compuesto por planos paralelos equidistantes, y estos elementos eran designados los indivisibles de la superficie y del volumen respectivamente."

3D World

HASTA LAS MASCOTAS QUERRÁN APRENDER

Concluyendo

Sugerencias

Cilindros y Conos (Desarrollo 2)

Cilindros y Conos (Desarrollo 1)

Cilindros y Conos 2

Cilindros y Conos 1

Relacionando

Volumen de Cilindros y Conos

Algo de Historia